计算库层(同chapter3.4 5)
Triton 提供了高性能的计算库,开发者可以利用这些库进行高效操作。例如,标准的Add(向量加法)、 GEMM(矩阵乘法)等操作可以使用 Triton 的编程模型实现,利用自定义内存访问模式和自动调优功能获得更佳性能。
参考仓库地址:triton
向量加法的实现示例代码如下:
"""
Vector Addition
===============
In this tutorial, you will write a simple vector addition using Triton.
In doing so, you will learn about:
* The basic programming model of Triton.
* The `triton.jit` decorator, which is used to define Triton kernels.
* The best practices for validating and benchmarking your custom ops against native reference implementations.
"""
# %%
# Compute Kernel
# --------------
import torch
import triton
import triton.language as tl
@triton.jit
def add_kernel(x_ptr, # *Pointer* to first input vector.
y_ptr, # *Pointer* to second input vector.
output_ptr, # *Pointer* to output vector.
n_elements, # Size of the vector.
BLOCK_SIZE: tl.constexpr, # Number of elements each program should process.
# NOTE: `constexpr` so it can be used as a shape value.
):
# There are multiple 'programs' processing different data. We identify which program
# we are here:
pid = tl.program_id(axis=0) # We use a 1D launch grid so axis is 0.
# This program will process inputs that are offset from the initial data.
# For instance, if you had a vector of length 256 and block_size of 64, the programs
# would each access the elements [0:64, 64:128, 128:192, 192:256].
# Note that offsets is a list of pointers:
block_start = pid * BLOCK_SIZE
offsets = block_start + tl.arange(0, BLOCK_SIZE)
# Create a mask to guard memory operations against out-of-bounds accesses.
mask = offsets < n_elements
# Load x and y from DRAM, masking out any extra elements in case the input is not a
# multiple of the block size.
x = tl.load(x_ptr + offsets, mask=mask)
y = tl.load(y_ptr + offsets, mask=mask)
output = x + y
# Write x + y back to DRAM.
tl.store(output_ptr + offsets, output, mask=mask)
# %%
# Let's also declare a helper function to (1) allocate the `z` tensor
# and (2) enqueue the above kernel with appropriate grid/block sizes:
def add(x: torch.Tensor, y: torch.Tensor):
# We need to preallocate the output.
output = torch.empty_like(x)
assert x.is_cuda and y.is_cuda and output.is_cuda
n_elements = output.numel()
# The SPMD launch grid denotes the number of kernel instances that run in parallel.
# It is analogous to CUDA launch grids. It can be either Tuple[int], or Callable(metaparameters) -> Tuple[int].
# In this case, we use a 1D grid where the size is the number of blocks:
grid = lambda meta: (triton.cdiv(n_elements, meta['BLOCK_SIZE']), )
# NOTE:
# - Each torch.tensor object is implicitly converted into a pointer to its first element.
# - `triton.jit`'ed functions can be indexed with a launch grid to obtain a callable GPU kernel.
# - Don't forget to pass meta-parameters as keywords arguments.
add_kernel[grid](x, y, output, n_elements, BLOCK_SIZE=1024)
# We return a handle to z but, since `torch.cuda.synchronize()` hasn't been called, the kernel is still
# running asynchronously at this point.
return output
# %%
# We can now use the above function to compute the element-wise sum of two `torch.tensor` objects and test its correctness:
torch.manual_seed(0)
size = 98432
x = torch.rand(size, device='cuda')
y = torch.rand(size, device='cuda')
output_torch = x + y
output_triton = add(x, y)
print(output_torch)
print(output_triton)
print(f'The maximum difference between torch and triton is '
f'{torch.max(torch.abs(output_torch - output_triton))}')
# %%
# Seems like we're good to go!
# %%
# Benchmark
# ---------
#
# We can now benchmark our custom op on vectors of increasing sizes to get a sense of how it does relative to PyTorch.
# To make things easier, Triton has a set of built-in utilities that allow us to concisely plot the performance of our custom ops.
# for different problem sizes.
@triton.testing.perf_report(
triton.testing.Benchmark(
x_names=['size'], # Argument names to use as an x-axis for the plot.
x_vals=[2**i for i in range(12, 28, 1)], # Different possible values for `x_name`.
x_log=True, # x axis is logarithmic.
line_arg='provider', # Argument name whose value corresponds to a different line in the plot.
line_vals=['triton', 'torch'], # Possible values for `line_arg`.
line_names=['Triton', 'Torch'], # Label name for the lines.
styles=[('blue', '-'), ('green', '-')], # Line styles.
ylabel='GB/s', # Label name for the y-axis.
plot_name='vector-add-performance', # Name for the plot. Used also as a file name for saving the plot.
args={}, # Values for function arguments not in `x_names` and `y_name`.
))
def benchmark(size, provider):
x = torch.rand(size, device='cuda', dtype=torch.float32)
y = torch.rand(size, device='cuda', dtype=torch.float32)
quantiles = [0.5, 0.2, 0.8]
if provider == 'torch':
ms, min_ms, max_ms = triton.testing.do_bench(lambda: x + y, quantiles=quantiles)
if provider == 'triton':
ms, min_ms, max_ms = triton.testing.do_bench(lambda: add(x, y), quantiles=quantiles)
gbps = lambda ms: 3 * x.numel() * x.element_size() / ms * 1e-6
return gbps(ms), gbps(max_ms), gbps(min_ms)
# %%
# We can now run the decorated function above. Pass `print_data=True` to see the performance number, `show_plots=True` to plot them, and/or
# `save_path='/path/to/results/' to save them to disk along with raw CSV data:
benchmark.run(print_data=True, show_plots=True, save_path="output")
结果:
tensor([1.3713, 1.3076, 0.4940, ..., 0.9584, 0.7074, 1.3011], device='cuda:0')
tensor([1.3713, 1.3076, 0.4940, ..., 0.9584, 0.7074, 1.3011], device='cuda:0')
The maximum difference between torch and triton is 0.0
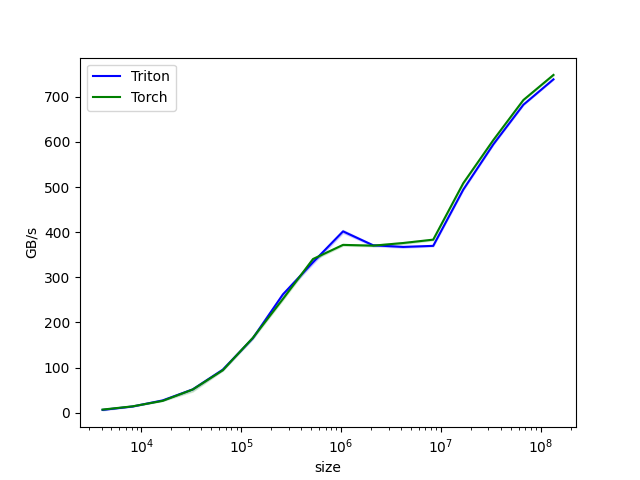
vector-add-performance:
size Triton Torch
0 4096.0 6.237563 6.942373
1 8192.0 13.806741 14.124138
2 16384.0 27.306667 26.284491
3 32768.0 51.738946 51.468063
4 65536.0 95.440773 94.070810
5 131072.0 165.216809 165.913932
6 262144.0 262.143998 252.061538
7 524288.0 333.233892 340.446769
8 1048576.0 401.753280 371.835454
9 2097152.0 370.953018 370.085627
10 4194304.0 367.274371 375.945969
11 8388608.0 369.649426 383.447069
12 16777216.0 494.318016 508.501939
13 33554432.0 594.617812 604.037490
14 67108864.0 682.344488 692.781332
15 134217728.0 738.572773 748.332490
 下面将实现一个融合的 softmax 操作,该操作在处理特定类型的矩阵时,性能显著优于 PyTorch 的原生实现。具体而言,当矩阵的行可以适应 GPU 的 SRAM 时,融合内核可以减少内存访问并提高计算效率。通过这个例子,我们将学习内核融合的好处以及 Triton 中的归约操作。
下面将实现一个融合的 softmax 操作,该操作在处理特定类型的矩阵时,性能显著优于 PyTorch 的原生实现。具体而言,当矩阵的行可以适应 GPU 的 SRAM 时,融合内核可以减少内存访问并提高计算效率。通过这个例子,我们将学习内核融合的好处以及 Triton 中的归约操作。
融合的 softmax实现示例代码如下:
"""
Fused Softmax
=============
In this tutorial, you will write a fused softmax operation that is significantly faster
than PyTorch's native op for a particular class of matrices: those whose rows can fit in
the GPU's SRAM.
In doing so, you will learn about:
* The benefits of kernel fusion for bandwidth-bound operations.
* Reduction operators in Triton.
"""
# %%
# Motivations
# -----------
#
# Custom GPU kernels for elementwise additions are educationally valuable but won't get you very far in practice.
# Let us consider instead the case of a simple (numerically stabilized) softmax operation:
import torch
import triton
import triton.language as tl
from triton.runtime import driver
def is_hip():
return triton.runtime.driver.active.get_current_target().backend == "hip"
def is_cdna():
return is_hip() and triton.runtime.driver.active.get_current_target().arch in ('gfx940', 'gfx941', 'gfx942',
'gfx90a', 'gfx908')
def naive_softmax(x):
"""Compute row-wise softmax of X using native pytorch
We subtract the maximum element in order to avoid overflows. Softmax is invariant to
this shift.
"""
# read MN elements ; write M elements
x_max = x.max(dim=1)[0]
# read MN + M elements ; write MN elements
z = x - x_max[:, None]
# read MN elements ; write MN elements
numerator = torch.exp(z)
# read MN elements ; write M elements
denominator = numerator.sum(dim=1)
# read MN + M elements ; write MN elements
ret = numerator / denominator[:, None]
# in total: read 5MN + 2M elements ; wrote 3MN + 2M elements
return ret
# %%
# When implemented naively in PyTorch, computing :code:`y = naive_softmax(x)` for :math:`x \in R^{M \times N}`
# requires reading :math:`5MN + 2M` elements from DRAM and writing back :math:`3MN + 2M` elements.
# This is obviously wasteful; we'd prefer to have a custom "fused" kernel that only reads
# X once and does all the necessary computations on-chip.
# Doing so would require reading and writing back only :math:`MN` bytes, so we could
# expect a theoretical speed-up of ~4x (i.e., :math:`(8MN + 4M) / 2MN`).
# The `torch.jit.script` flags aims to perform this kind of "kernel fusion" automatically
# but, as we will see later, it is still far from ideal.
# %%
# Compute Kernel
# --------------
#
# Our softmax kernel works as follows: each program loads a set of rows of the input matrix X strided by number of programs,
# normalizes it and writes back the result to the output Y.
#
# Note that one important limitation of Triton is that each block must have a
# power-of-two number of elements, so we need to internally "pad" each row and guard the
# memory operations properly if we want to handle any possible input shapes:
@triton.jit
def softmax_kernel(output_ptr, input_ptr, input_row_stride, output_row_stride, n_rows, n_cols, BLOCK_SIZE: tl.constexpr,
num_stages: tl.constexpr):
# starting row of the program
row_start = tl.program_id(0)
row_step = tl.num_programs(0)
for row_idx in tl.range(row_start, n_rows, row_step, num_stages=num_stages):
# The stride represents how much we need to increase the pointer to advance 1 row
row_start_ptr = input_ptr + row_idx * input_row_stride
# The block size is the next power of two greater than n_cols, so we can fit each
# row in a single block
col_offsets = tl.arange(0, BLOCK_SIZE)
input_ptrs = row_start_ptr + col_offsets
# Load the row into SRAM, using a mask since BLOCK_SIZE may be > than n_cols
mask = col_offsets < n_cols
row = tl.load(input_ptrs, mask=mask, other=-float('inf'))
# Subtract maximum for numerical stability
row_minus_max = row - tl.max(row, axis=0)
# Note that exponentiation in Triton is fast but approximate (i.e., think __expf in CUDA)
numerator = tl.exp(row_minus_max)
denominator = tl.sum(numerator, axis=0)
softmax_output = numerator / denominator
# Write back output to DRAM
output_row_start_ptr = output_ptr + row_idx * output_row_stride
output_ptrs = output_row_start_ptr + col_offsets
tl.store(output_ptrs, softmax_output, mask=mask)
# %%
# We can create a helper function that enqueues the kernel and its (meta-)arguments for any given input tensor.
device = torch.cuda.current_device()
properties = driver.active.utils.get_device_properties(device)
NUM_SM = properties["multiprocessor_count"]
NUM_REGS = properties["max_num_regs"]
SIZE_SMEM = properties["max_shared_mem"]
WARP_SIZE = properties["warpSize"]
target = triton.runtime.driver.active.get_current_target()
kernels = {}
def softmax(x):
n_rows, n_cols = x.shape
# The block size of each loop iteration is the smallest power of two greater than the number of columns in `x`
BLOCK_SIZE = triton.next_power_of_2(n_cols)
# Another trick we can use is to ask the compiler to use more threads per row by
# increasing the number of warps (`num_warps`) over which each row is distributed.
# You will see in the next tutorial how to auto-tune this value in a more natural
# way so you don't have to come up with manual heuristics yourself.
num_warps = 8
# Number of software piepling stages.
num_stages = 4 if SIZE_SMEM > 200000 else 2
# Allocate output
y = torch.empty_like(x)
# pre-compile kernel to get register usage and compute thread occupancy.
kernel, num_programs = kernels.get(BLOCK_SIZE, (None, 0))
if kernel is None:
kernel = softmax_kernel.warmup(y, x, x.stride(0), y.stride(0), n_rows, n_cols, BLOCK_SIZE=BLOCK_SIZE,
num_stages=num_stages, num_warps=num_warps, grid=(1, ))
kernel._init_handles()
n_regs = kernel.n_regs
size_smem = kernel.metadata.shared
if is_hip():
# NUM_REGS represents the number of regular purpose registers. On CDNA architectures this is half of all registers available.
# However, this is not always the case. In most cases all registers can be used as regular purpose registers.
# ISA SECTION (3.6.4 for CDNA3)
# VGPRs are allocated out of two pools: regular VGPRs and accumulation VGPRs. Accumulation VGPRs are used
# with matrix VALU instructions, and can also be loaded directly from memory. A wave may have up to 512 total
# VGPRs, 256 of each type. When a wave has fewer than 512 total VGPRs, the number of each type is flexible - it is
# not required to be equal numbers of both types.
if is_cdna():
NUM_GPRS = NUM_REGS * 2
# MAX_NUM_THREADS represents maximum number of resident threads per multi-processor.
# When we divide this number with WARP_SIZE we get maximum number of waves that can
# execute on a CU (multi-processor) in parallel.
MAX_NUM_THREADS = properties["max_threads_per_sm"]
max_num_waves = MAX_NUM_THREADS // WARP_SIZE
occupancy = min(NUM_GPRS // WARP_SIZE // n_regs, max_num_waves) // num_warps
else:
occupancy = NUM_REGS // (n_regs * WARP_SIZE * num_warps)
occupancy = min(occupancy, SIZE_SMEM // size_smem)
num_programs = NUM_SM * occupancy
kernels[BLOCK_SIZE] = (kernel, num_programs)
num_programs = min(num_programs, n_rows)
# Create a number of persistent programs.
kernel[(num_programs, 1, 1)](
y,
x,
x.stride(0),
y.stride(0),
n_rows,
n_cols,
)
return y
# %%
# Unit Test
# ---------
# %%
# We make sure that we test our kernel on a matrix with an irregular number of rows and columns.
# This will allow us to verify that our padding mechanism works.
torch.manual_seed(0)
x = torch.randn(1823, 781, device='cuda')
y_triton = softmax(x)
y_torch = torch.softmax(x, axis=1)
assert torch.allclose(y_triton, y_torch), (y_triton, y_torch)
# %%
# As expected, the results are identical.
# %%
# Benchmark
# ---------
#
# Here we will benchmark our operation as a function of the number of columns in the input matrix -- assuming 4096 rows.
# We will then compare its performance against (1) :code:`torch.softmax` and (2) the :code:`naive_softmax` defined above.
@triton.testing.perf_report(
triton.testing.Benchmark(
x_names=['N'], # argument names to use as an x-axis for the plot
x_vals=[128 * i for i in range(2, 100)], # different possible values for `x_name`
line_arg='provider', # argument name whose value corresponds to a different line in the plot
line_vals=['triton', 'torch'], # possible values for `line_arg``
line_names=[
"Triton",
"Torch",
], # label name for the lines
styles=[('blue', '-'), ('green', '-')], # line styles
ylabel="GB/s", # label name for the y-axis
plot_name="softmax-performance", # name for the plot. Used also as a file name for saving the plot.
args={'M': 4096}, # values for function arguments not in `x_names` and `y_name`
))
def benchmark(M, N, provider):
x = torch.randn(M, N, device='cuda', dtype=torch.float32)
stream = torch.cuda.Stream()
torch.cuda.set_stream(stream)
if provider == 'torch':
ms = triton.testing.do_bench(lambda: torch.softmax(x, axis=-1))
if provider == 'triton':
ms = triton.testing.do_bench(lambda: softmax(x))
gbps = lambda ms: 2 * x.nelement() * x.element_size() * 1e-9 / (ms * 1e-3)
return gbps(ms)
benchmark.run(show_plots=True, print_data=True, save_path="output")
结果:
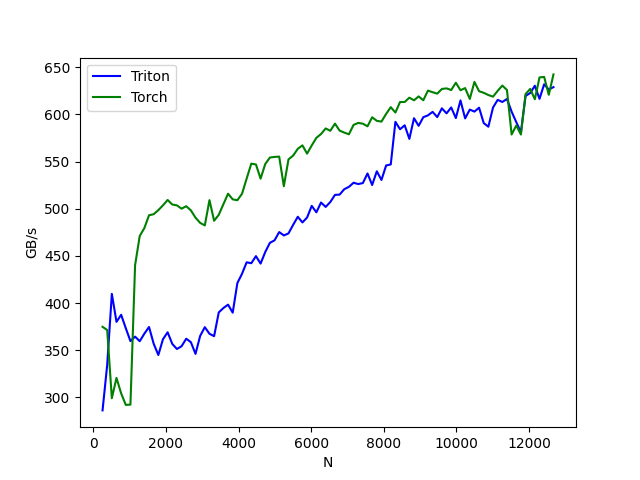
softmax-performance:
N Triton Torch
0 256.0 286.304086 374.914120
1 384.0 334.484465 371.506107
2 512.0 409.811791 299.262763
3 640.0 380.141194 320.723956
4 768.0 387.645576 304.382499
5 896.0 373.444696 292.122508
6 1024.0 359.742054 292.430046
7 1152.0 364.509882 440.223322
...
96 12544.0 626.395424 620.854101
97 12672.0 628.975394 642.458547
矩阵乘法的实现示例代码如下:
import torch
import triton
import triton.language as tl
import time
# Define matrix multiplication kernel using Triton
@triton.jit
def matmul_kernel(
A, B, C, M, N, K, BLOCK_M: tl.constexpr, BLOCK_N: tl.constexpr, BLOCK_K: tl.constexpr,
):
pid = tl.program_id(0)
row = pid // (N // BLOCK_N)
col = pid % (N // BLOCK_N)
offs_m = row * BLOCK_M + tl.arange(0, BLOCK_M)
offs_n = col * BLOCK_N + tl.arange(0, BLOCK_N)
offs_k = tl.arange(0, BLOCK_K)
a_ptrs = A + offs_m[:, None] * K + offs_k[None, :]
b_ptrs = B + offs_k[:, None] * N + offs_n[None, :]
accum = tl.zeros((BLOCK_M, BLOCK_N), dtype=tl.float32)
for k in range(0, K, BLOCK_K):
a = tl.load(a_ptrs)
b = tl.load(b_ptrs)
accum += tl.dot(a, b)
a_ptrs += BLOCK_K
b_ptrs += BLOCK_K * N
c_ptrs = C + offs_m[:, None] * N + offs_n[None, :]
tl.store(c_ptrs, accum)
def matmul(a, b):
num_iters = 300
M, K = a.shape
N = b.shape[1]
C = torch.zeros((M, N), dtype=torch.float32, device='cuda')
# Compile and run Triton kernel
grid = (M // 32, N // 32)
start = time.time()
print("[Matrix Multiply Using Triton] - Starting...")
print(f"MatrixA({M},{K}), MatrixB({K},{N})")
for _ in range(num_iters):
matmul_kernel[grid](a, b, C, M, N, K, BLOCK_M=32, BLOCK_N=32, BLOCK_K=32)
torch.cuda.synchronize()
end = time.time()
# Calculate performance metrics
elapsed_time = end - start
time_per_iteration = elapsed_time * 1000 / num_iters
flops = 2.0 * M * N * K * num_iters
gflops = (flops / elapsed_time) / 1e9
# Output performance results
print(f"Triton Performance= {gflops:.2f} GFlop/s, Time= {time_per_iteration:.3f} msec")
return C
# Matrix sizes
M, N, K = 320, 320, 320
# Initialize matrices
A = torch.randn((M, K), dtype=torch.float16, device='cuda')
B = torch.randn((K, N), dtype=torch.float16, device='cuda')
# Call the matmul function
C = matmul(A, B)
print(f"Output matrix C: {C}")
结果:
[Matrix Multiply Using Triton] - Starting...
MatrixA(320,320), MatrixB(320,320)
Triton Performance= 52.65 GFlop/s, Time= 1.245 msec
Output matrix C: tensor([[ 20.6646, -1.4497, 1.6400, ..., 11.9098, 12.1640, -13.7652],
[ 10.9663, -3.8929, 12.4444, ..., -9.7939, -19.5267, -21.4840],
[ 1.5969, -0.4670, 48.2527, ..., -18.8371, 22.3166, -23.5707],
...,
[ 0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[ 0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[ 0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000]],
device='cuda:0')